TL;DR Science: Exploration of Probability, Part 3

A  two-way table, expresses data based on two variables which often form categories. The coincidence of these two categories forms a conditional event.

Ex. 

The following table includes the coincidence of two categories: grade level (9th, 10th, 11th, or 12th grade) and pet preference (dog, cat, bird)

A survey was taken at your high school from the student population, which asked them about pet preferences. The two way table shows the findings. 

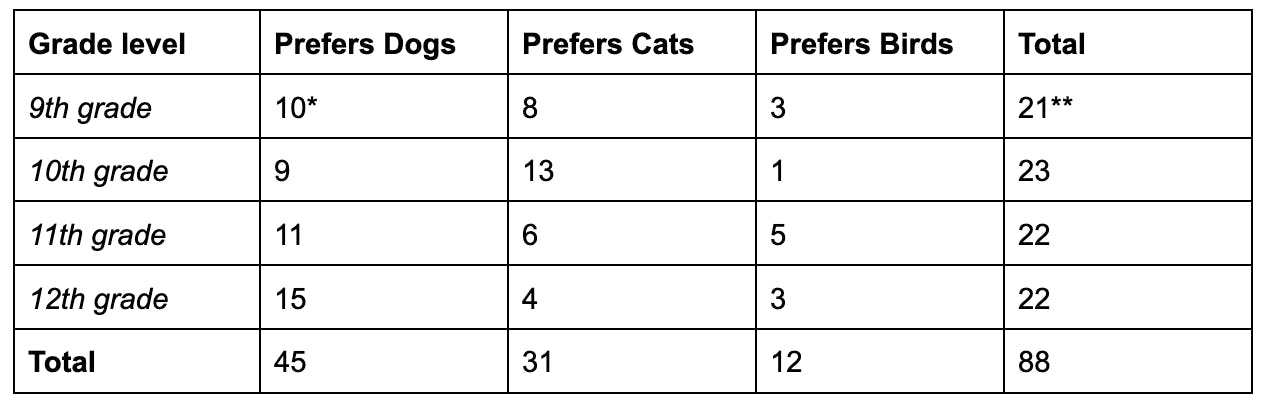
Referring to the table, a conditional event in this case could be P(Prefers Dogs given is in 9th grade) or P(Dog | 9th grader). That means, from a pool of freshmen, what is the probability that one is likely to prefer dogs?

We can determine that the probability of P(Dog | 9th grader) is 1021 by referring to the table using the following system:

1. Refer to the specific row of 9th graders, since we are taking from a pool of 9th graders
   
   
   
2. Refer to the specific cell which gives the number of 9th graders who prefer dogs.

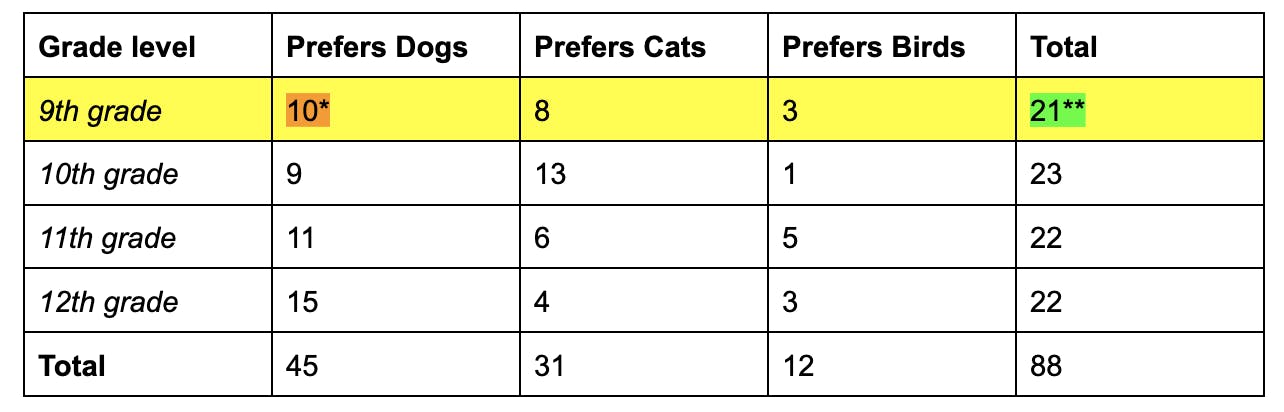
Since the probability of an event is defined by: 

probability = (number of possible successful outcomes)/(number of possible outcomes)

Since the number of possible successes is 10 (9th grade ⋂ Prefers Dogs) (refers to orange highlighted number) and the number of possible outcomes is 21 (9th grade)(refers to green highlighted number), P(Dog | Freshman) = 10/21. 

This examples leads us to the law of conditional probabilities: 

P(A | B) = P(A ∩ B)/P(B)

“The probability of event A given event B is equal to the probability of event A and B divided by the probability of event B”.

This law is evidenced in the formula for dependent events: P(A ∩ B) =P(A) • P(B|A) (if you recall from the last article) or P(A ∩ B) =P(B) • P(A|B) (if you merely switch up the letters). Let’s take P(A ∩ B) =P(B) • P(A|B) for the sake of simplicity. If you divide both sides by P(B), you get the rule of P(A|B) from above.

We can also demonstrate the use of this formula through the two way table example above.

From the rule above, we can prove that P(Dog | 9th grader) =  1021  by dividing P(Dog ∩ 9th grader) by P(9th grade). Let me demonstrate: 

P(A | B) = P(A ∩ B)/P(B)    (given)

P(Dog | 9th grader) = P(Dog ∩ 9th grader)/P(9th grader) = (10/88*)/(21/88**)(refer to table)

Highlighted in orange (also starred *) is P(Dog ∩ 9th grader), while what is highlighted in green (also starred **) is P(9th grader) both are in terms of the total number of students, which is 88. So, the probability that a student prefers a dog AND is a 9th grader is 10 students out of 88 in total while the probability that a student is 9th grader is 21/88.

(10/88*)/(21/88**) = (10/88)*(88/21) (separate into two fractions - keep, change flip) 

=(10/21) (simplify)

So, P(A | B) = P(A ∩ B)/P(B) as evidenced above. An extension of this law can be taken from the law of dependent events: P(A ∩ B) =P(A) • P(B|A) in order to get rid of the P(A ∩ B) and break down the the formula all the way to events A, B, and B|A. This is called “Bayes’ Theorem”: 

P(A | B) = P(A) • P(B|A)P(B)

Unfortunately, we don’t have time left in this story to discuss Bayes’ Theorem, but if you are interested here is some further reading: https://www.investopedia.com/terms/b/bayes-theorem.asp