TL;DR Science: Numerical Analysis: The Unsung Hero of Science

In science, physical processes like chemical reactions or moving bodies are modelled using mathematics. The mathematical models used are ordinarily systems of equations that relate all the quantities being dealt with symbolically. These equations are said to hold for values of the variables that lie in a particular set like the real numbers or a subset of the real numbers. That means that the equations are continuous and can take infinitely many values. For example in Newton’s second law F = ma, a can be any positive or negative real number that can take values of 9, 9.991, 9.5264 etc. 

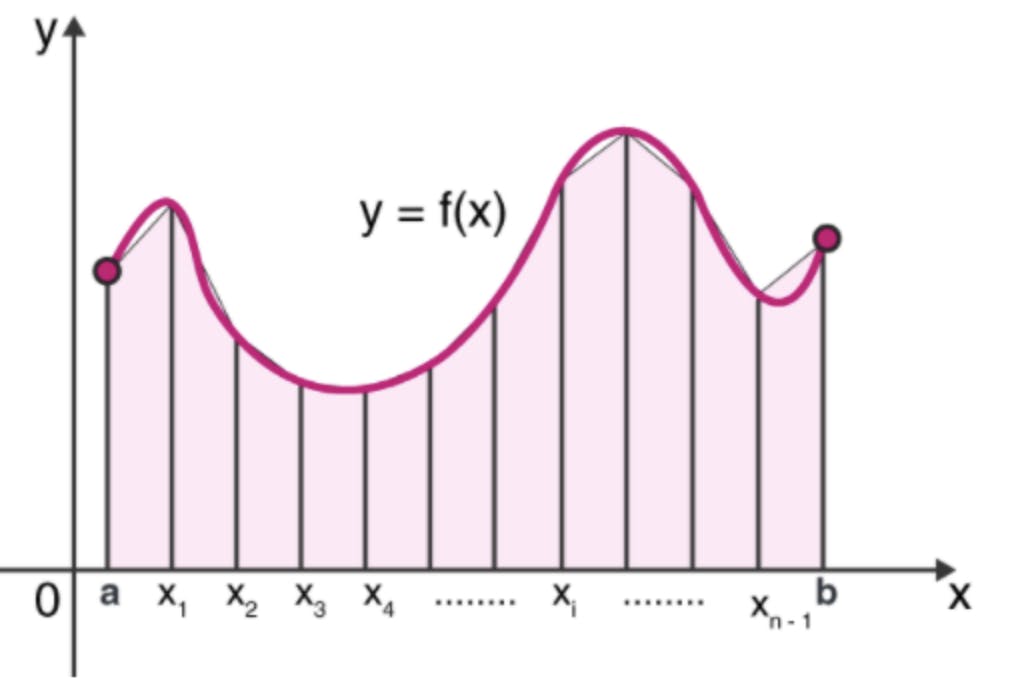
All that means is that if we want to figure out what the acceleration for a certain physics problem is, and the acceleration is not constant then we need to find a continuous function that solves the problem for any value of F or m. This continuity and the need to find a function of a certain type is simple in a lot of ideal physics problems but in real-world problems, we find that certain equations are not easily solvable analytically, meaning that the solution is a known function like x^2 or sinx or in some cases it can be proven that there is no analytical solution. But if such a problem arises in a physical system that we can observe, surely there must be a solution to the system of equations because we have observed something happening over time. 

This is where numerical analysis plays a key role. Numerical analysis breaks down complicated problems that arise when dealing with continuous systems and reduces them into simple numerical calculations, that is, processes like addition, subtraction etc. These processes cannot be conducted on a large scale by a human because of the time it would take and the mistakes that would arise in the calculations. A computer, though, can perform millions of numerical calculations a minutes. 

This method allows us to solve extremely complicated integrals or differential equations or linear algebra problems that model physical systems. The downside though is that you don’t get an exact solution at the end. This is because in order to reduce the equations to simple operations we have to perform a process called discretisation, that is dividing a continuous space into finite pieces. The more pieces there are the higher the accuracy of the numerical solution.

Example

Suppose we have the following integral: 

Int0-> 10 e^-x^2 dx

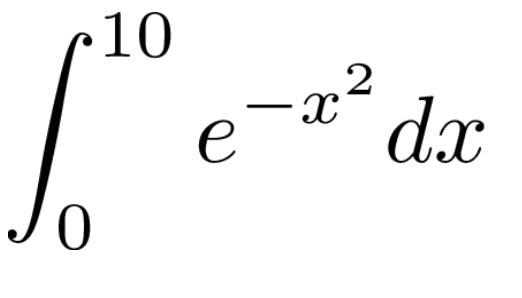
This is an integral that a calculus student would not be able to solve with any of the known integration techniques and in fact, this integral cannot be solved analytically at all. It is known as the Gaussian integral and is used in error analysis. 

Let’s say we discretise the space [0,10] into pieces delta x such that N * Δx = 10. That means we have divided the space into N pieces of equal size. Notice that using the definition of the definite integral for discrete values of x the integral reduces to the following sum:

Int = sum[i=1, N](e^(N*delta x)^2)* delta x.

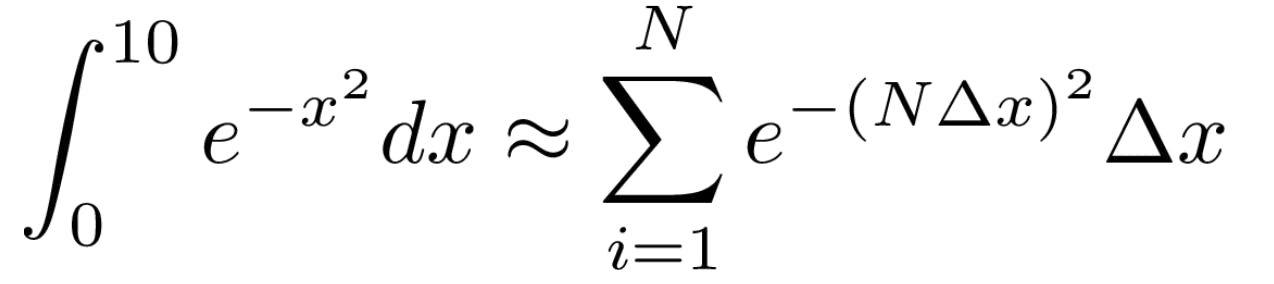
which is easily computable if programmed onto a computer.

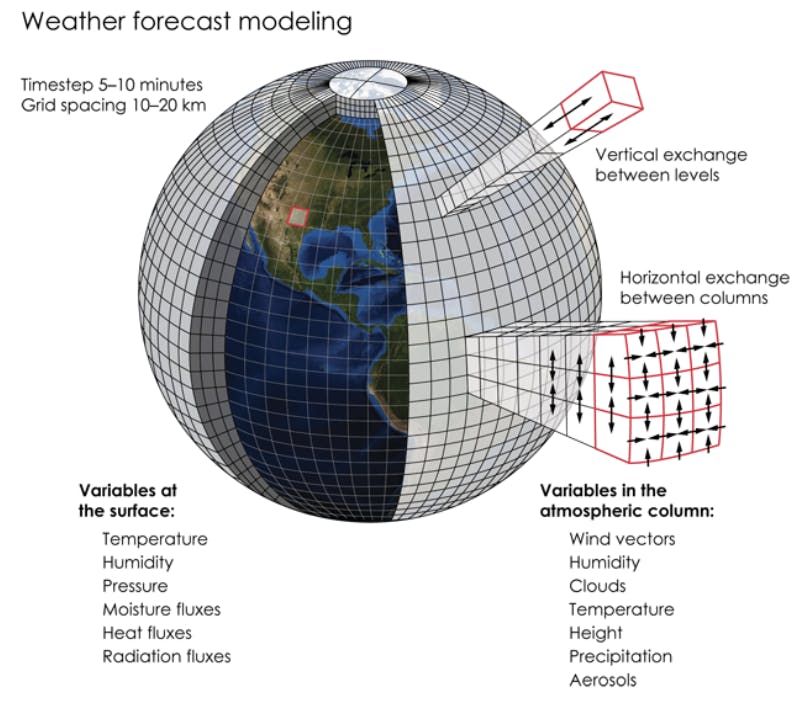
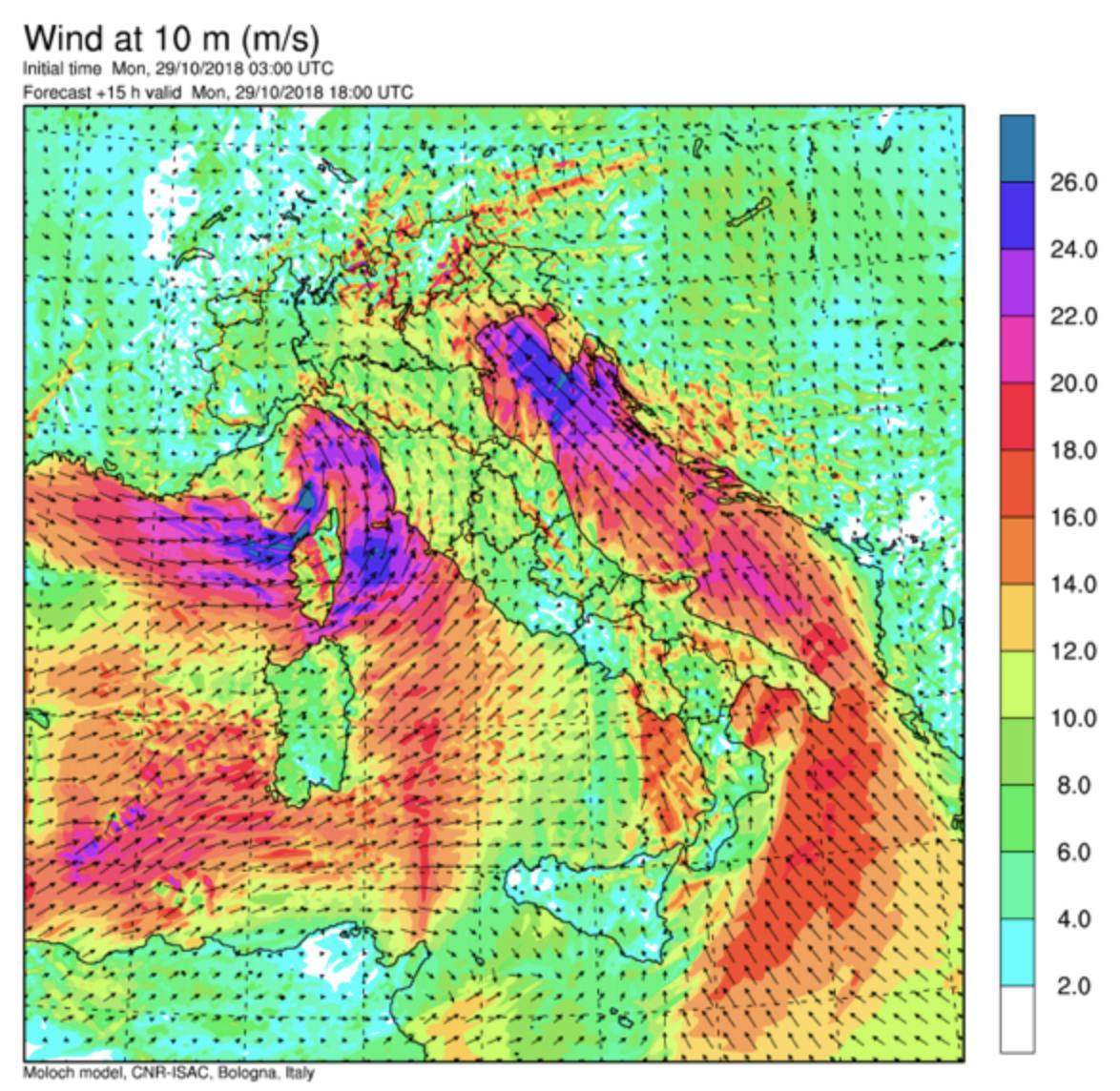
The impact of numerical analysis is very far-reaching. This method allows us to solve systems of equations, optimise single and multivariable functions, solve differential equations, compute integrals, do interpolation and extrapolation etc. This is what makes predicting the weather, calculating spacecraft trajectories and optimising flight paths possible. Finally, this method along with the development of computers made fields in physics that even the famous physicist Richard Feynman thought were a dead end possible while also opening up a whole new world of possibilities to chemists and biologists alike.

TLDR:

All physical systems are modelled using equations. Those equations in ideal situations have solutions that are described using continuous functions like that of the trajectory of a moving object. In the real world though, problems don’t always have simple functions as a solution(analytical solution). Using computers we can reduce even the hardest of problems into a set of finite numerical operations that a computer can do naturally. This method is called numerical analysis and the solution it provides us with is called a numerical solution. Without this method, weather forecasts and spacecraft wouldn’t be possible.

Sources:

Numerical Methods for Scientists and Engineers, Richard Hamming