TL;DR Science: Exploration of Probability, Part 2

When I finished the previous article about Probability (for a refresher, click this link), I was discussing the following law: 

P(A or B) = P(A) + P(B) - P(A and B) -or-  P(A ⋃ B) = P(A) + P(B) -P(A ∩ B)

While this law is quite useful in many situations, it may not always be necessary to use. For example, if the P(A ∩ B) =0 , the events A and B would be considered mutually exclusive, and thus you would not have to consider the intersection of the events. The law of mutually exclusive events is thus: 

P(A or B) = P(A) + P(B) - 0 -or-  P(A ⋃ B) = P(A) + P(B)

Thinking back to the example of students taking various science classes, the law of mutually exclusive events would be applicable if your school did not allow students to take multiple science classes. Thus, the probability of finding a person taking Bio and Chem would be 0.

* * *

Joint probabilities of events

As we know the symbol ∩ indicates intersection (which means “and”): when two events occur at the same time or consecutively. For example, let’s say we flip two coins consecutively and are hoping for heads and then tails. As we know, there is a 50% chance of both happening. Typically in order to find the probability of flipping two coins and finding two heads you would multiply their probabilities, writing the intersection of these two events as Heads ∩ Tails:

Ex.

P(Heads ∩ Tails) = 

0.5 • 0.5 = 0.25 

This may seem intuitive, but without the theory behind probability, it seems arbitrary. Let's explore this deeper. 

Conditional probability

A conditional event, an event that occurs given (or, is dependent on) the occurrence of another. The probability of A given B, ex., can be written as P(A|B), with the vertical bar ( | ) representing the word “given” or “is conditioned on”. To be clear, this means that a certain event, (A|B) can only occur when B occurs then A on the condition of B already having occurred. 

Independent events

Going back to the example above, we can explain the reason why we multiplied these two probabilities by thinking of the second heads as a conditional event, where

P(Heads and Tails) = P(Heads) • P(Tails given Heads), or:

P(Heads ∩ Tails) = P(Heads) • P(Tails | Heads), where: 

0.25 = 0.5 • .0.5

In this case, it may seem useless to express P(Tails | Heads) since P(Heads) equals P(Tails | Heads), since the conditional event (one tails given another heads) and the original event (one heads) are both equal to 0.5 - the probability does not change. So why shouldn’t we just get rid of P(Tails | Heads) and replace it with P(Tails) or P(Heads)? Well, there is no reason not to, since this is a case of independent events: one event, even when conditioned on another, has the same probability as the original event. 

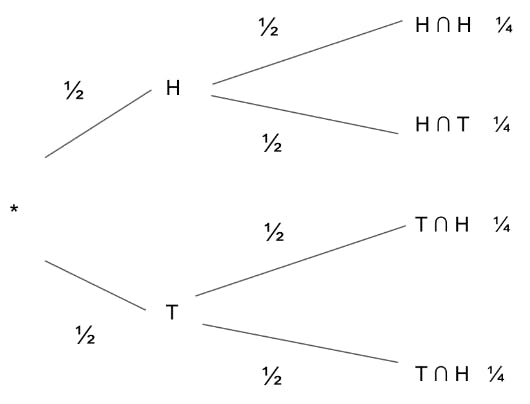
Above: P(Heads ∩ Heads) = P(Heads ∩ Tails) = P(Tails ∩ Tails) = P(Tails ∩ Heads) = ½ * ½ = ¼ 

However, we cannot make this generalization for every pair of events.

Dependent events

Dependent events are events in which a conditional event may not have the same probability as the original event. For example, for events A and B, the P(A|B) does not equal P(A). Imagine above if somehow the probability of tails given heads was somehow different from the original probability of heads (or tails).

Dependent events are commonly seen in places where you are dealing with a limited sample space and a lack of replacement. Let’s provide an illustration of this. 

Ex. Let’s say you have eight marbles: two white, two black, four blue. Thus, the probability of picking a white, black, or blue marble is:

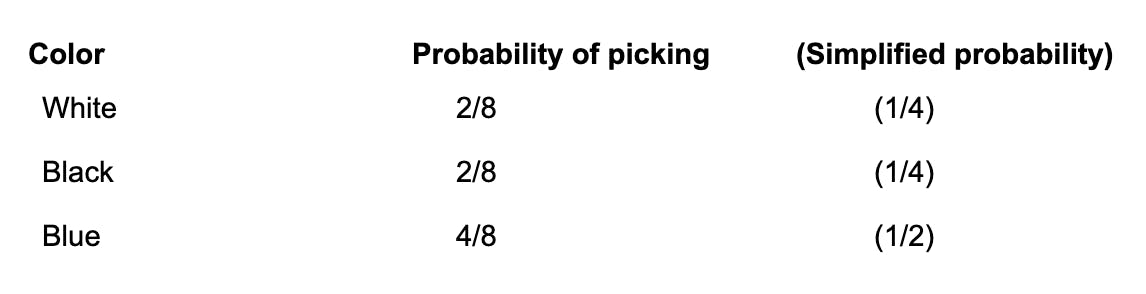
But, if you remove one of those marbles (i.e. pick another one without replacement), the whole probability matrix is going to be out of whack! For example, if I remove a white marble, the probability matrix will change as such: 

This is because I am picking from a bowl of marbles with one less marble than before, which not only impacts the probability of the white marbles but also the black and blue marbles as well. Thus, the probability of picking a white marble is going to decrease, but the probability of picking a black or blue marble is going to increase. 

Therefore, we can say with certainty that in the above scenario the probability of the conditional event (picking a white marble given already having picked a white marble) does not equal probability of the original event (picking a white marble). 

I.E. P(White | White) = 1/7 ≠        P(White) = 2/8

Thus, we cannot replace P(White) with P(White | White) in the formula to find P(White ∩ White) as we did above with the independent events. 

In conclusion, to summarize: