TL;DR Math: Probability Pt. 1
By Thomas P.
March 03, 2023 · 4 minute read
Mathematics
Statistics
Cognitive Science
Have you ever heard someone say, “There’s a 50/50 chance that ___ will occur”? Well, what does that actually mean and how can you apply the principles of probability to combine probabilities of multiple events? That is something we will explore in this article.
Introduction to probability and various rules
Let’s begin by first defining what probability is. Probability is the likelihood that something will occur typically expressed as a fraction (less than or equal to 1), a percent (less than or equal to 100%), or a decimal (also less than or equal to 0). Remember that a percent is merely a probability expressed in decimal form multiplied by 100. If a probability is 0, it will never happen, if it is 1 then it will always happen, and if a probability is equal to .5 then it is just as likely to happen as it is not to happen.
The formula for probabilities is
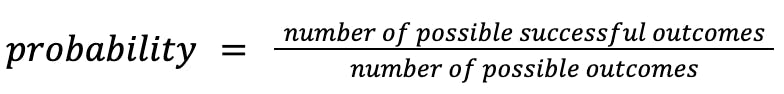
since a probability is always merely the likelihood that success will occur given all of the possible outcomes that can possibly occur.
For short, we can use probability notation, which gives the letter P (standing for “probability of”) outside another letter (standing in as the name of the event), such as with P(A) = 1, in which we would read the notation as “The Probability of Event A equals 1”.
A very common event that occurs that has a very simple probability is a flip of a fair coin, which has a simple probability of 50% if either heads or tails (1 possible successful outcome out of two possible outcomes - 1/2).
Ex:
Event in which heads (H) occurs:
P(H) = 1/2
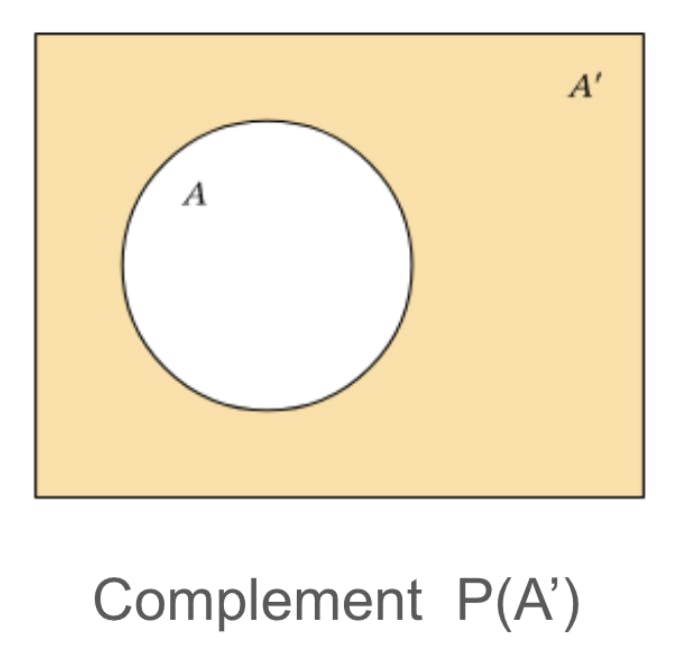
The probability of any event NOT occurring, or the complement of an event, is the probability of experiencing another possible outcome that would not be considered as success, and is naturally 1 (the total probability of all outcomes possibly occurring) minus the probability of the event:
The complement of Event A (P(A’) - “A prime”) is:
P(Not A) = 1 - P(A) (or) P(A’) = 1 - P(A)
Ex.
The probability of flipping a coin and achieving heads is ½ (0.5), so therefore the probability of heads not happening is:
P(H’) = 1 - 0.5 = 0.5
Addition Rules
Ex. Let’s say you are in a school where there are multiple different types of sciences you can take. 40% of students take Biology, 30% take Chemistry, 20% take both Biology and Chemistry, and the rest take only Environmental Science.
Let’s say you are conducting a survey of your own. Based on the probabilities above, what is the combined probability that someone is taking Biology OR Chemistry? In this case, you are going to have to add the probabilities, taking into account that there are some people that take both Biology and Chemistry (that you must subtract from this count, or else they will be counted twice). This leads us to the the next law:
P(A or B) = P(A) + P(B) - P(A and B)
We can use the symbols “⋃” (union (“or”) - i.e. the combined probabilities of both events, occurring in conjunction or by themselves) and “∩” (intersection (“and”) - i.e. the probability of both events occurring in conjunction only) for the words and & or respectively.
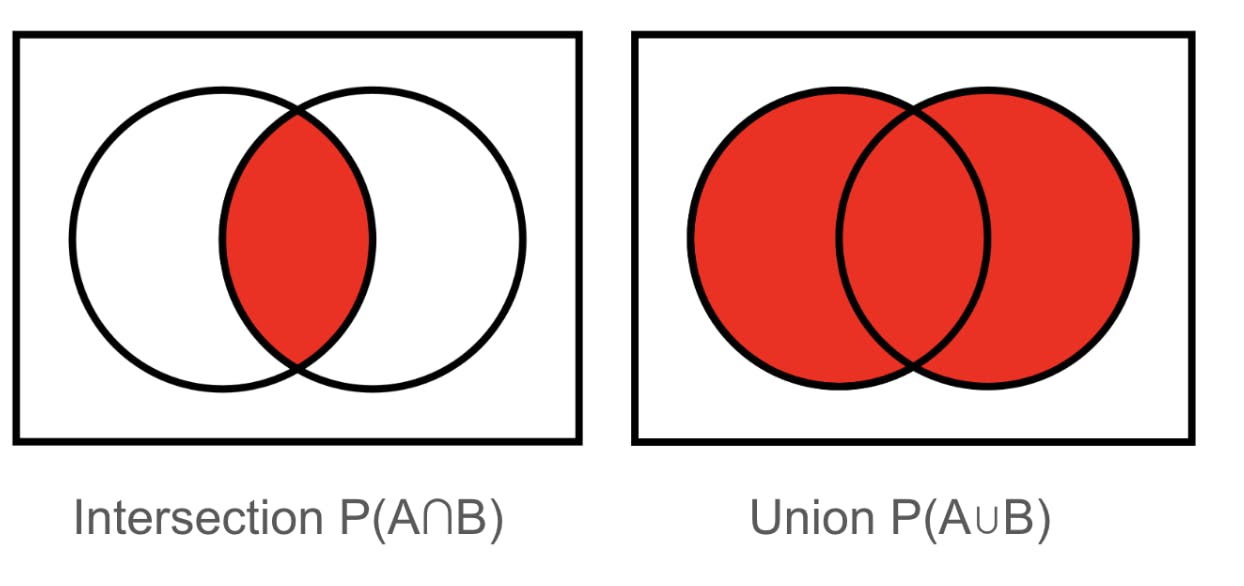
Essentially, if the events overlap, the union of the two is the probability of both (A or B) combined minus the probability of the two happening at the same time (A and B).
P(A ⋃ B) = P(A) + P(B) -P(A ∩ B)
Given the example above, we know:
P(Bio) = 0.4
P(Chem) = 0.3
P(Bio and Chem) / P(Bio ∩ Chem) = 0.2
Given the law above, we know therefore, the P(Bio or Chem) / P(Bio ⋃ Chem) =
P(Bio ⋃ Chem) = P(Bio) + P(Chem) -P(Bio ∩ Chem)
0.5 = 0.4 + 0.3 - 0.2
The probability that someone takes Biology or Chemistry is therefore 0.5 or 50%.
While it always takes more time and practice for you to become good with probability, I hope that this provides you with a simple, non-exhaustive, exposure to a few basic probability rules.
Further Reading:
https://medium.com/data-comet/probability-rules-cheat-sheet-e24b92a9017f
Did you enjoy this article?
About The Author
Thomas is a student at Eastside High School.